In fact, many optical systems image objects in space on an image plane, called the space image on the plane, such as telescopic objective lens, photographic objective lens, etc., belong to this category.
The object points in space are distributed at different distances from the incident pupil of the optical system. The imaging principle of these points is the same as that of plane objects.
As shown in Figure 1, B1,B2,B3,B4 are any points in space, point P is the center of incident pupil, point P' is the center of exit pupil, and A'B' is the image plane, which is called scene plane. The plane AB conjugated with the scene plane in object space is called the alignment plane.
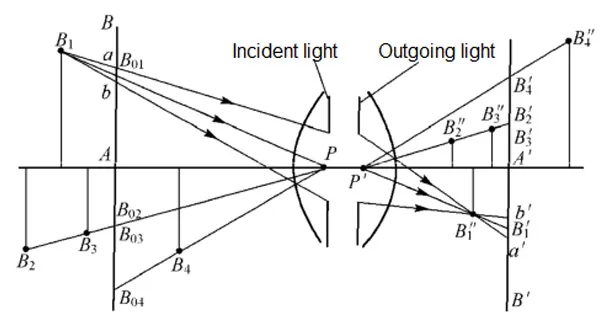
The lines of points B1,B2,B3,B4 and the center point P of the incident pupil are the main rays of these points respectively. The conjugate points of these points in image space are B1",B2",B3",B4"respectively. The main rays passing through these points intersect with the scene plane A'B' at points B1',B2',B3',B4', respectively.
Obviously, the two points B2 and B3 located on the same main ray B2P coincide with their counterparts B2' and B3' in the scene plane. Thus, the points B2 and B3 are conjugated with the projection of the points B2' and B3' in the direction of the main ray in the alignment plane.
Therefore, the image of space points on the plane can be obtained as follows: take the center point of incident pupil P as the perspective center, that is, take point P as the projection center, and project space points B1,B2,B3,B4 to the alignment plane along the direction of the main ray. Then the conjugate points B1',B2',B3',B4' of the projection points on the scene plane are the plane image of space points.
When pupil has a certain size, the beam full of incident pupil emitted by point B1 intersects with the alignment plane as a dispersion spot a'b', and the conjugate image on the scene plane is also a dispersion spot ab, which is the projection of space image point B1 "on the scene plane.
Similarly, all space points located outside the scene plane can generate A dispersion spot on the alignment plane, and conjugate image can also be obtained on the scene plane A 'b '.
As can be seen from Figure 1, the size of ab or a'b' is related to the diameter of incident pupil. As the diameter of incident pupil decreases, these dispersion spots also decrease. When the diameter of the incident pupil is small to a certain extent, the diffuse spot ab can be regarded as a point, and its conjugate image αb' can also be regarded as a point.
Similarly, for points B2,B3 and B4 on the scene plane, the dispersion spots can also be considered as point images B2',B3' and B4' due to the decrease of incident pupil. Therefore, clear images of space points outside the alignment plane can be obtained on the scene plane A'B'.
As mentioned above, the imaging of object space points is equivalent to taking the center of incident pupil as the projection center and the main light as the projection line, so that the space points are projected on the alignment plane and then the imaging is done on the scene plane.
Or in the image space, with the center of the exit pupil as the projection center, each space image point is projected along the main light on the scene plane, or the plane image of the space object point can be formed.


















 EN
EN





